Is German Train Travel Faster North↔South or East↔West?
Map of Speed on route vs Distribution of Routes split by direction

Many years ago I used to write short stories. For many of these I now look back and cringe. For this question, I suspect I shall look back at it similarly. However I think it's important to record this otherwise I'll have nothing to look back on, which is worse.

As it often the case when I am in Germany, the topic of (painful) train travel came up, and in particular: is it quicker to go North↔South than East↔West? Me being me, I wondered if I could answer this with data.

The TLDR is: maaaaaaybe. You can see the notebook for more detail on where I got to, but my approach was, in summary:

  1. Find all cities in Germany.
  2. Create all pairs of cities that traverse a North↔South or East↔West boundary.
  3. Find shortest travel time between these cities.
  4. Compute speed by dividing travel time by crow-flies distance between cities.
  5. Group routes into North↔South or East↔West and plot a distribution.

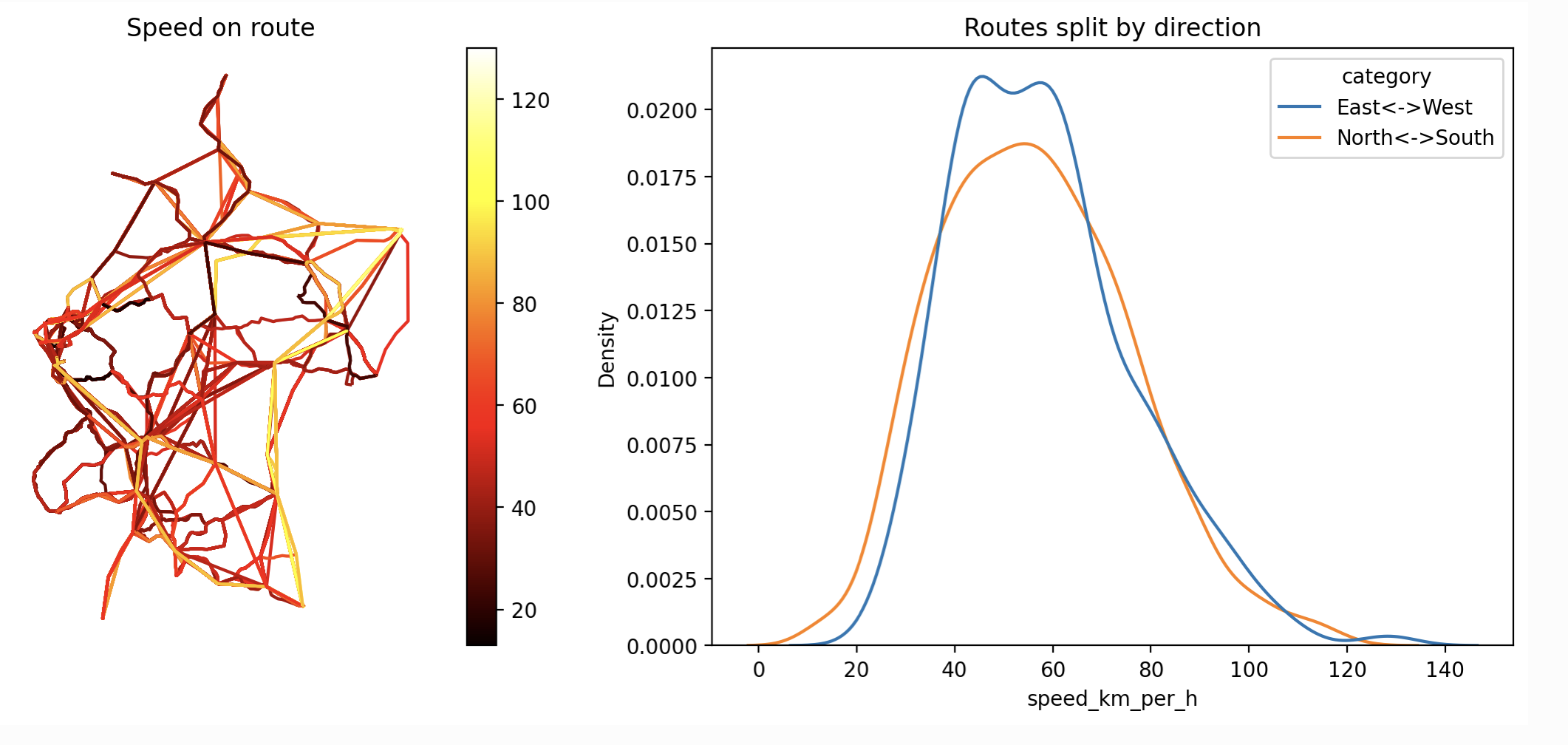
The overall outcome can be seen in the image at top: there doesn't seem to be an obvious difference. I could be more rigorous about this by doing a statistical test, but I think there are bigger issues to deal with.

As is often the case, doing an initial investigation just reveals problems with the definition of the question 😀. For example, if I look at the distribution of crow-fly distances, by normalising to speed, and I ignoring something of interest?


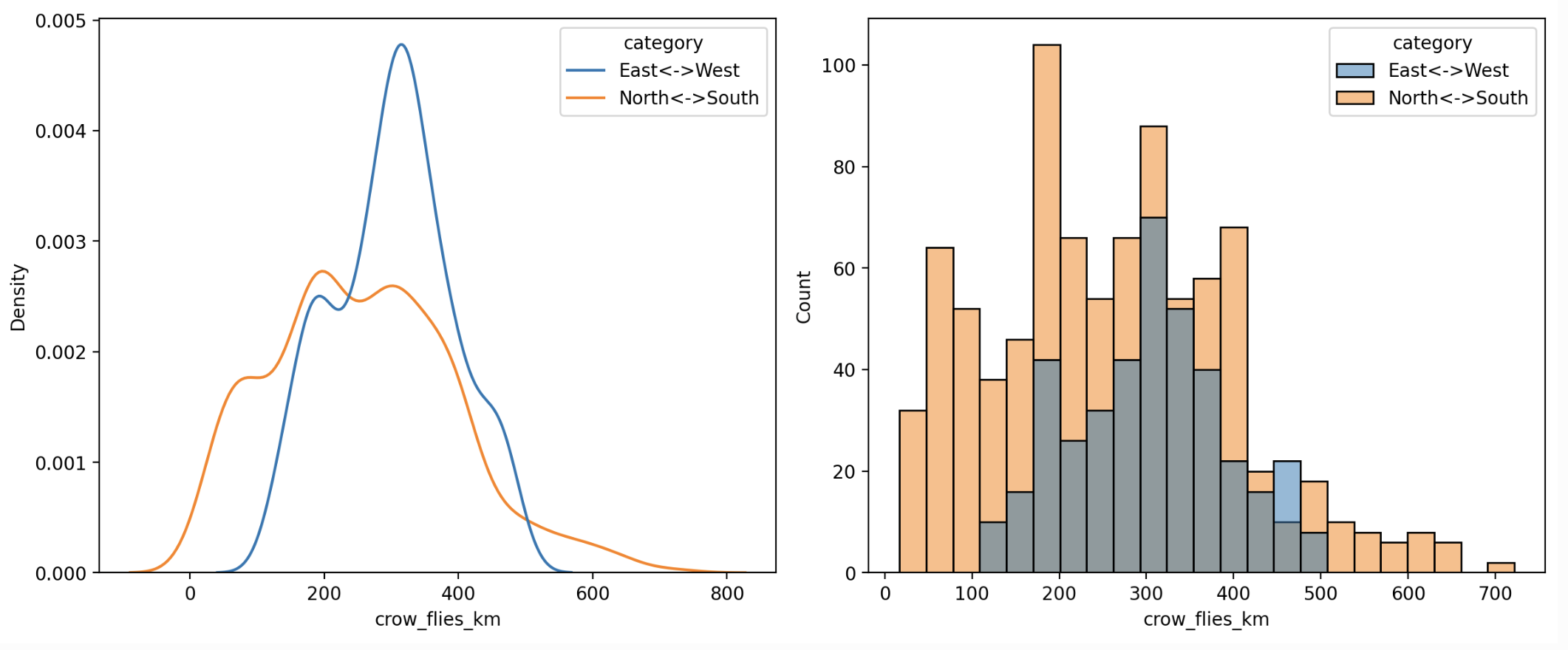
Is it maybe that East↔West journeys are generally longer than North↔South? Perhaps not. If you look at the map of cities you can see there is a cluster of cities near the North↔South boundary.


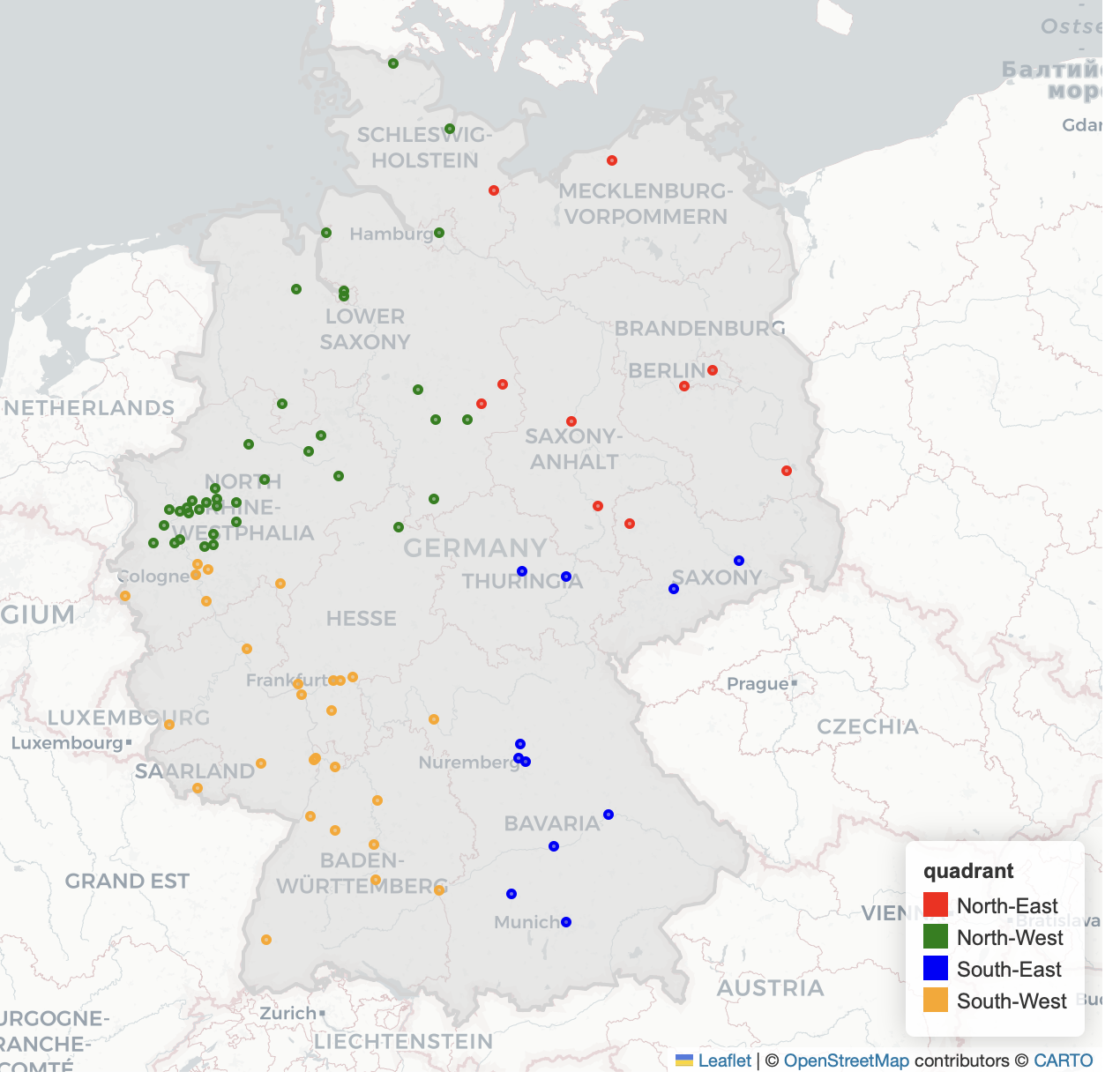
This will introduce a bias in that it will produce a bunch of routes that are short.

There is also the issue that I am (arbitrarily) choosing 9am on 10th Jan 2026 as the departure time.

I only wanted to spend a day on this, so I won't take this further for now. However, if I did, I'd probably want to instead do something like:

  • Prepare:
    1. Take the area of Germany and subdivide it into areas using H3 or A5.
    2. Use the centroid of each of these to categorise into quadrants.
    3. Find all pairs as before, but this time between centroids of areas.
  • Collect: for each pair, for 24h throughout the day, in 1h steps, find fastest travel time.
  • Analyse:
    • Do something like before but, since there may still be bias from how often routes of different lengths occur between areas, I probably want to bucket by route length and compute an average.
    • This will give me more of an unbiased summary. However, since population distribution isn't unbiased, I probably want to rebias the sample by wieghting towards where more people live. This gives more of an idea of what a typical experience would be.

Anyways, I'm not gonna do all that now 😀.

One thing I will probably do sooner is re-use the motis server setup. It was a massive pain trying out various public/private libraries/services for travel times, and finding various versions of broken-ness or "please talk to sales" road-blocks.

Motis worked really well out-of-the-box and could easily handle all of Germany on my Macbook Air; only took about 20 minutes to import the data, and then lookups were fast. Also, even though I was using it for API only, the nice UI for inspecting / debugging was a great bonus.


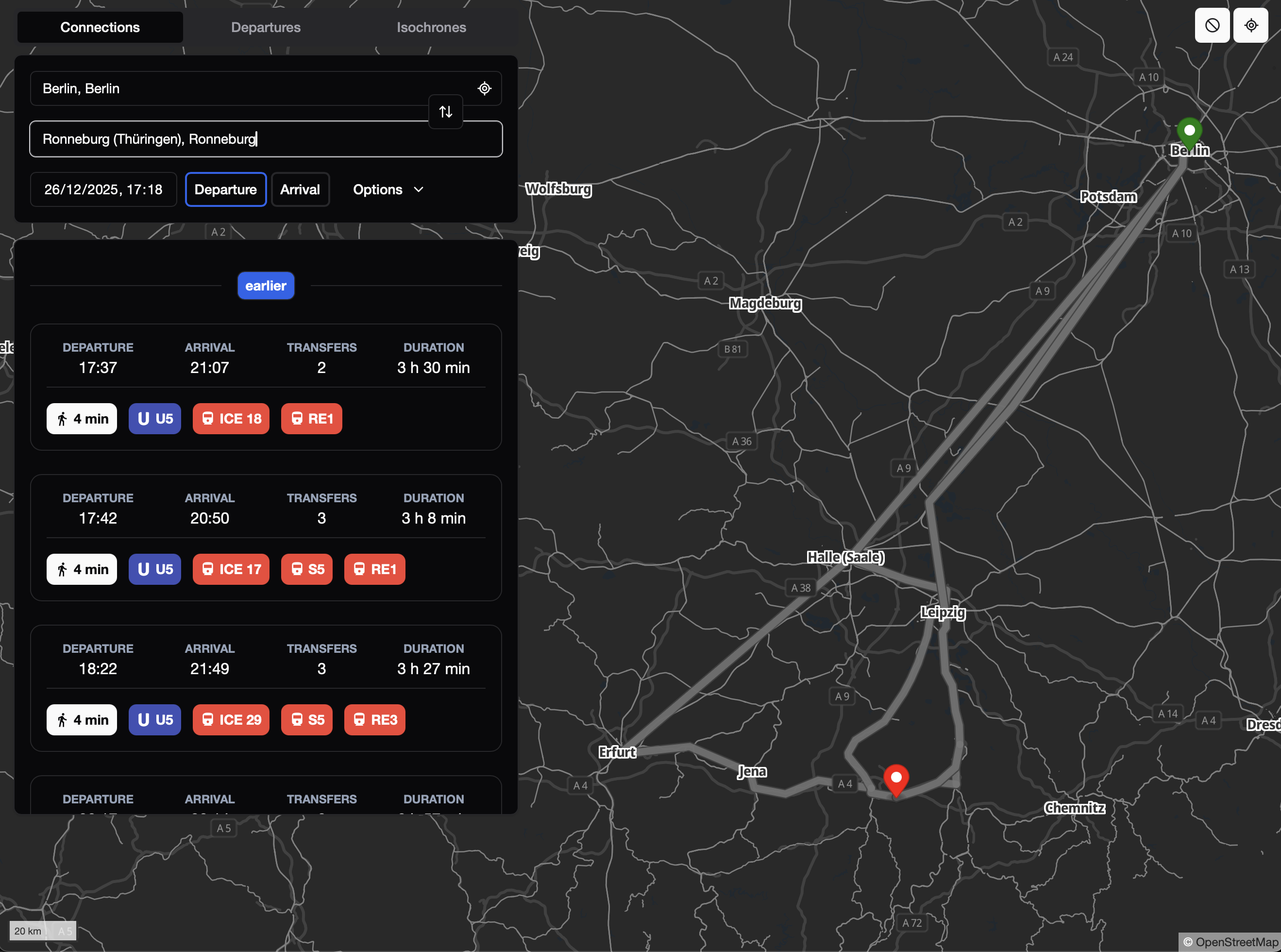
Even better, it's based on open-data for Maps and Timetables!