Over the holidays I was thinking about where I am with the Biscuits project. The Linzer version has gotten to the point where I have a lot of the core bits of technical knowledge required, and I "merely" need to understand the aesthetics, if I wanted to copy the original artist.

Whilst it is good to attempt to copy to learn, I am now a bit uneasy with it as a goal. This is partly because the habit of "Computing People" copying "Artistic people" is becoming a bit rude in the current race-to-the-bottom of AI Art. However, it's also because I have some other ideas I wanna explore. So, I'm gonna do that instead.

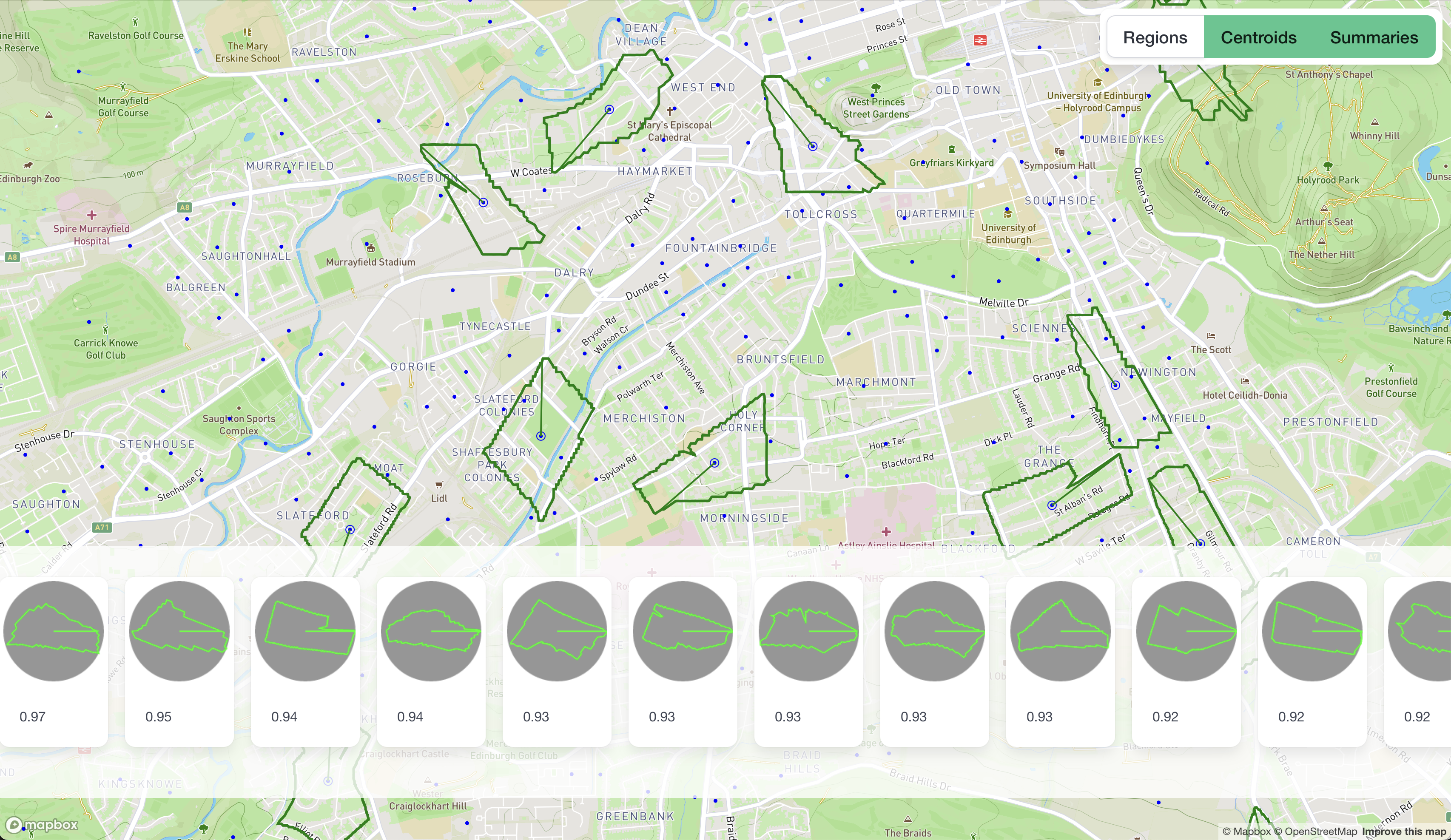
This doesn't change the need for good core parts. To that end I've been putting together something that I call a "Region Summary". This is intended to be a lossy-but-simple summary of a Region, that still allows comparison between them.

This is "lossy" because when a shape has nooks, if these end up doubling-back from the pov of the Centroid, then they will be lost. However, it retains more detail than just finding the Convex Hull.

This Summary has some nice properties such as being able to use to find similar Regions. Here is an example where we treat it is a 360-element Vector and find those Regions within a certain "similarity" where similarity = (1.0 - avg(diff between distances at each Bearing)):

This version only has Regions for Edinburgh but you can have a play yourself here: linzer.houseofmoran.io.

This now gives a substrate on top of which I can build other stuff.

However, part of the reason I am writing this up here is because this is almost certainly not a new problem / solution. I wanted to have a go myself to better understand it, but I am very much up for suggestions of alternatives, or even a well-known name for this technique.

(I can be contacted on Mastodon or Bluesky).